
李群李代数学习笔记(一):从群到群

李群 : 流形 + 群。左平移
。左不变矢量场 。 李代数 :矢量空间
单参子群 :
曲线 若满足 则称 为 的单参数子群
重要关系: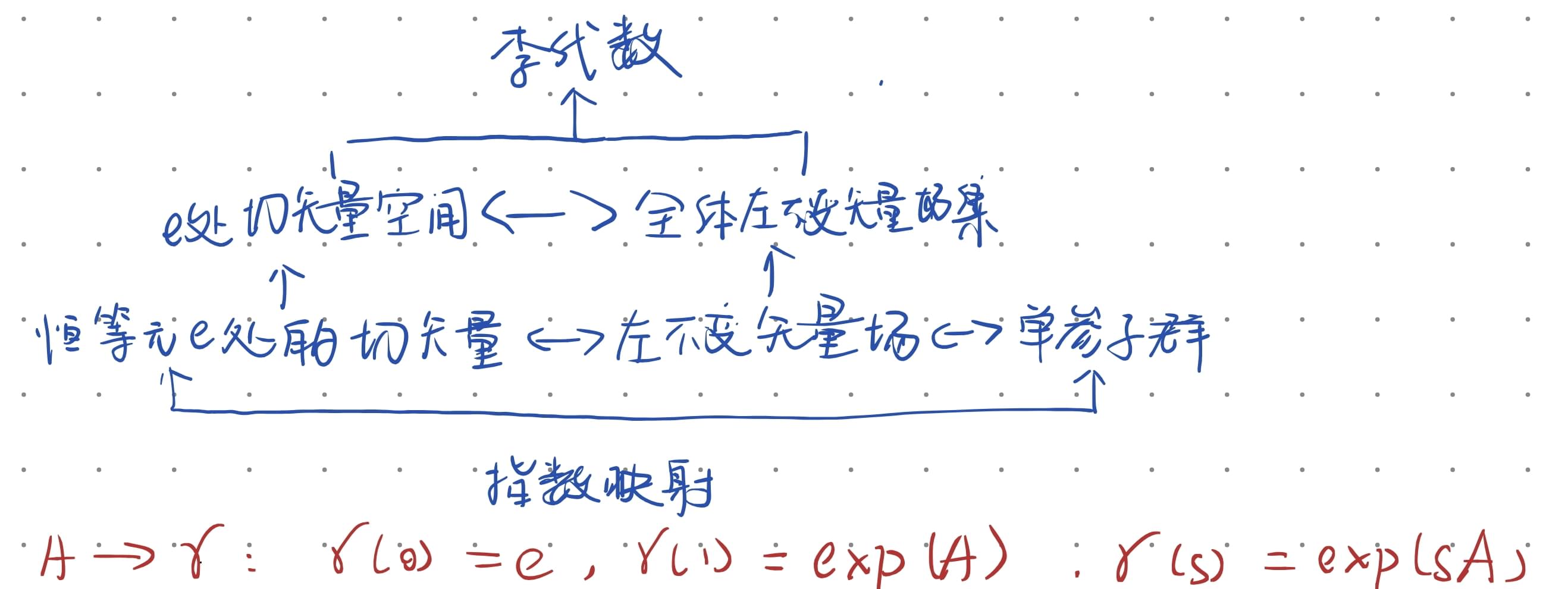
- 常用李群李代数 :
| 符号 | 李群名称 | 连通性 | 矩阵 | 维数 | 其李代数的矩阵 |
|---|---|---|---|---|---|
| 一般线性群(实) | 不连通 | ||||
| 一般线性群(复) | 连通 | ||||
| 特殊线性群(实) | 连通 | 行列式为 1 的 | |||
| 特殊线性群(复) | 连通 | 行列式为 1 的 | |||
| 正交群 | 不连通 | ||||
| 转动群 (特殊正交群) | 连通 | 行列式为 1 的正交实矩阵 | |||
| 洛伦兹群 | 不连通 | ||||
| 固有洛伦兹群 | 连通 | ||||
| 酉群 | 连通 | ||||
| 特殊酉群 | 连通 | 行列式为 1 的 |
李代数的结构常量:
李变换群与killing 场: 定义李变换群 :设G为李群,M为流形,
称为M上的一个李变换群,若:
(a). 对于任意g微分同胚
(b). 为同态映射定义从李群
到变换群 的上述同态映射 为 的一个实现, M 称为实现空间。若此同态为同构, 则称忠实实现。 定义李群
在 上的一个实现 称为 的一个表示, 若 为矢量空间, 且 为线性变换。这时 称为表示空间。若忠实实现是表示, 则为忠实表示。 定理 :
的等度规群的李代数 同构于其上全体 killing 矢量场 的李代数; 当每一Killing 场都完备时
重要关系: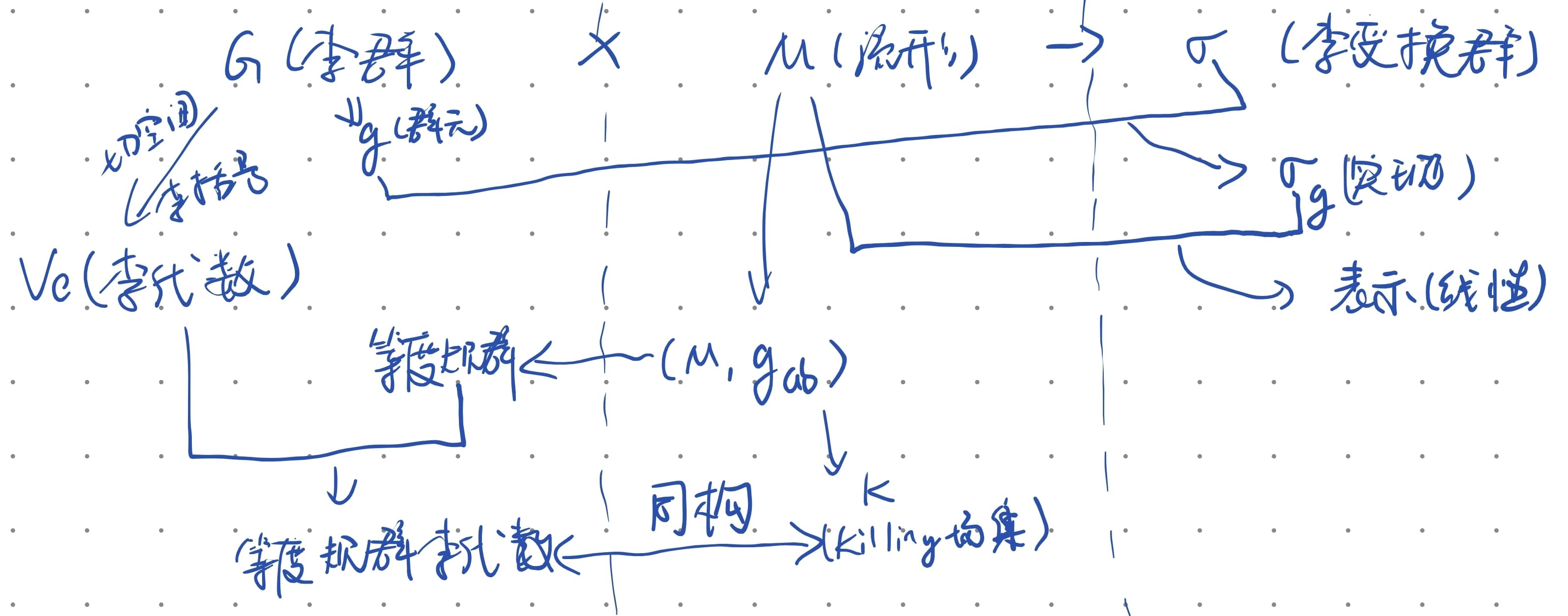
- 标题: 李群李代数学习笔记(一):从群到群
- 作者: 辰虎
- 创建于 : 2025-11-05 16:13:49
- 更新于 : 2025-12-12 11:40:35
- 链接: https://www.chenhuhuhu.space/2025/11/05/李群李代数学习笔记(一):从群到群/
- 版权声明: 本文章采用 CC BY-NC-SA 4.0 进行许可。
评论
